词向量的前世今生
Published:
神经网络掀起了人工智能的浪潮,深度学习的热度也逐步盖过了机器学习。深度学习(Deep Learning)并不是一个新的概念,早在上个世纪七八十年代,深度神经网络(Deep Neural Netword)就诞生了。但由于数据集、运算能力的限制,深度学习经历了很长的低潮期,直到最近才在语音和图像应用上产生了突破性进展。不同于语音和图像领域,深度学习在自然语言处理(NLP)领域还没能表现出全面领先于传统统计机器学习方法的能力。不过,目前已有的一些研究也展露了深度学习在NLP应用上的潜力,词向量(word embedding)正是其中最基本也最广泛应用的。词向量目前常见的应用有:
- 使用训练出的词向量作为输入特征,提升现有系统,如应用在情感分析、词性标注、语言翻译等神经网络中的输入层。
- 直接从语言学的角度对词向量进行应用,如使用向量的距离表示词语相似度、query相关性等。
本文试图以词向量的发展为脉络,从早期Bengio的Neural Probabilistic Language Models[1],到Mikolov关于Word2Vec的两篇论文Efficient Estimation of Word Representations in Vector Space[2]和Distributed Representations of Words and Phrases and their Compositionality[3],介绍涉及的网络结构、公式原理和开源工具。
Why Word Embedding?
机器学习模型要求输入是数字,因此自然语言处理问题要转化为机器学习的问题首先需要把自然语言数学符号化。NLP早期最常见的方法是One-hot Representation,这种方法把词转化成一个很长的稀疏向量,向量的维度等于词表大小,在向量中只有一个维度是1,其他都是0。One-hot稀疏表示法简洁,但也导致任意两个词之间都是孤立的。

语音、图像数据可以编码为高维度、稠密的向量,并且编码方式会影响语音、图像任务的性能。基于此,Hinton、Bengio、Milokov等提出了自然语言的Distributed representation,这种表示法可以把词映射到连续实数向量空间,且相似词在该空间中位置相近。有两种常见的途径获得Distributed representation,一种是 count-based方法( Latent Semantic Analysis),一种是predictive方法(neural probabilistic language models)。简单来说,Count-based方法在大语料集上计算词语的共现统计特征,然后把这些统计特征映射到低维空间成为低维、稠密向量;Predictive方法训练语言模型,直接尝试从学习词向量(是模型的参数)来通过邻居词估计目标词。
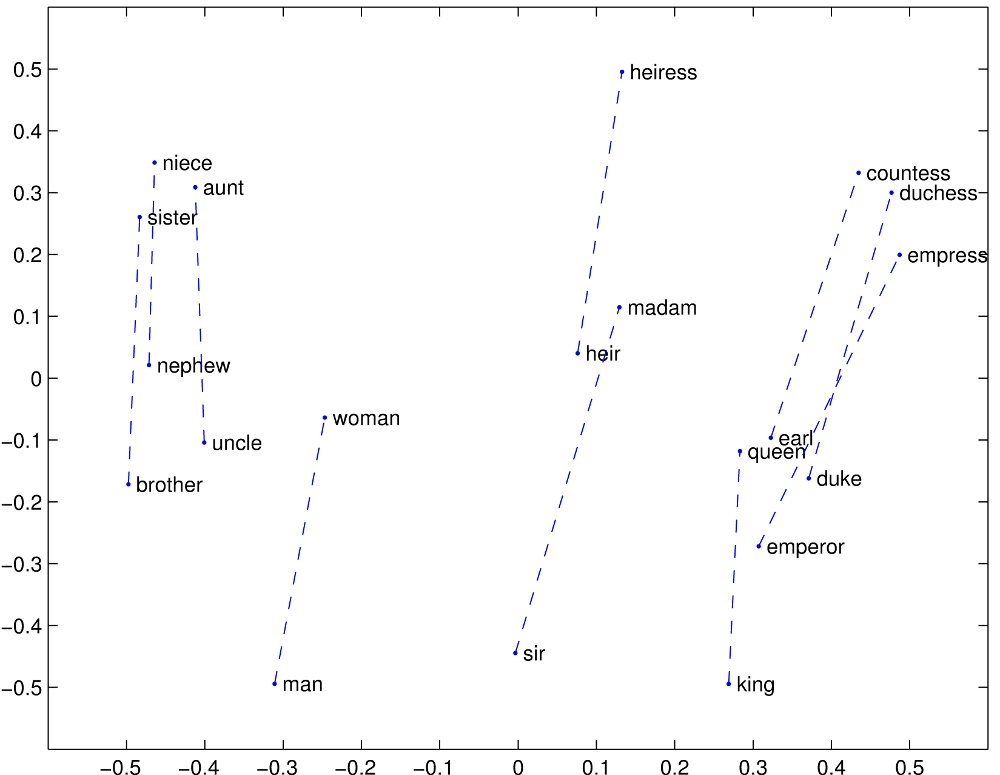
前世
Word2Vec算法使Distributed representation真正受到学术界、工业界的认可,它属于predictive方法,传承自Bengio的”Neural Probabilistic Language Models”[1]。NNLM是Distributed representation for words早期的重要工作,Word2Vec的很多方面受到该篇论文启发。文章提出了一个3层的网络结构(embedding输入层,tanh隐层,softmax输出层),通过最大化词序列的联合概率来学习word embedding。
背景知识
NNLM的目标函数是给定上文时下一个词的条件概率,该目标函数源于统计语言模型(statistical model of language)。一般地,统计语言模型将一个句子(由多个词构成的序列)的出现概率建模为:
\[\widehat{P}(w_{1}^{T})= \prod_{t=1}^{T}\widehat{P}(w_{t}|w_{1}^{t-1})\]计算统计语言模型的句子概率的计算复杂度是$O(N^T)$,N为语料中词的个数(vocabulary size,中文一般是2万~4万),T为句子长度(一般小于20)。
统计语言模型的计算复杂度太高,在早期实践中采用的是简化版本n-gram语言模型。n-gram模型可直接通过统计词频来计算,计算复杂度 - ,n一般取值2、3、4。n-gram模型的缺点是需要事先保存所有的概率值,工程上还涉及到对稀疏组合平滑化的操作。
\[\widehat{P}(w_{t}|w_{1}^{t-1})\approx \widehat{P}(w_{t}|w_{t-n+1}^{t-1})\]使用机器学习的观点看待求解给定上下文求下一个词的条件概率,目标函数为:
\[\widehat{P}(w|Context(w))=F(w,Context(w),\theta)\]使用对数最大似然算法(Maximum Log-Likelihood Esimation)进行参数估计:
\[L(\theta)=\sum_{w\in C}log p(w|Context(w))\]因此,通过选择合适的模型可以减小参数 - 的尺寸。事实上,Word2Vec受到广泛认可正是因为它在大幅提高了模型训练速度的同时,保证了较好的模型精度。从统计语言模型到NNLM,再到Word2Vec的过程也是一个以精度为约束提高训练速度的过程。
NNLM
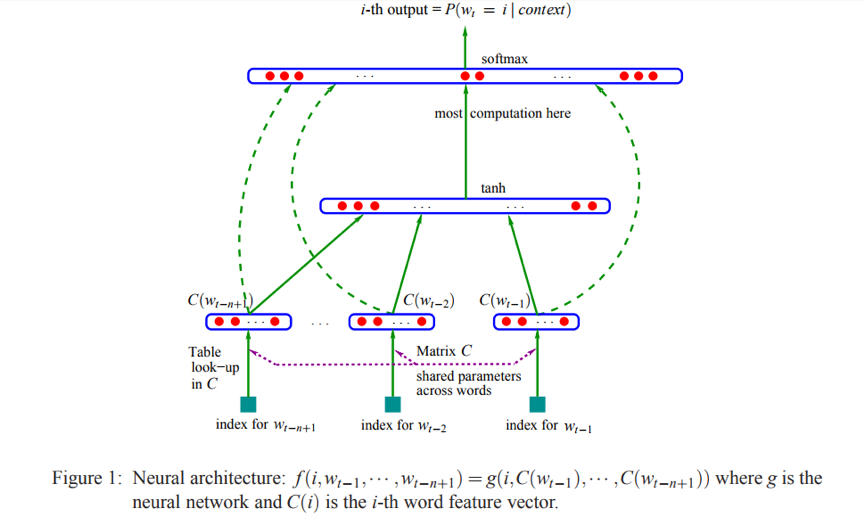
| 上图是NNLM的网络结构图,输入是target word的context(前n个词在矩阵C中的index,等价于在vocabulary中的index),输出是一个长度为$ | V | $的向量,其中第i维代表target word为$i$ ($i$同样是词在vocabulary中的index)在当前context下的条件概率。矩阵$C$是NNLM的关键部分,论文中原文是: |
In practice, $C$ is represented by a $ V $ * m matrix of free parameters. $C$ being shared across all the words in the context.
| 实际上,$C$矩阵存储的就是语料中所有词的词向量,它的行数$ | V | $是语料中词的个数,列数m为词向量的长度。上图$g$代表的是神经网络的映射(mapping),由图可知它包括了tanh层和softmax层。NNLM的目标函数为: |
其中,$b$是output层的bias;$W$是当词向量和output层有直接连接(direct connections)时的weight,对应NNLM网络结构图中的虚线,一般为0;$H, d$是tanh层(hidden层)的weight、bias;$U$是tanh层到output层的weight。(注意,隐藏层可以有多个神经元)
损失函数为:$L(\theta)=-\frac{1}{T}\sum_{t}logf(w_{t},w_{t-1},…,w_{t-n+1};\theta)+R(\theta)$, 其中 $R(\theta)$是正则惩罚项。
因此,$\theta=(b,d,W,U,H,C)$,对应的计算复杂度为:
\[|V|(1 + nm + h) + h(1 + (n - 1)m)=O(N(nm+h))\]其中,$N$为语料中词的个数,$h$为神经网络中隐藏层神经元的个数,$n$为context window的大小,$m$为词向量的维度。由此可见,NNLM将模型训练的计算复杂度由$O(N^n)$降低到$O(N*nm)$。论文中提到,在Associated Press 新闻数据集(1400w words),使用NNLM在40个CPU上训练5个epoch耗时约3周。
今生
2013年word2vec横空出世,背后的原理在Mikolov的两篇论文”Efficient Estimation of Word Representations in VectorSpace”[2], “Distributed Representations of Words and Phrases and their Compositionality”[3]中有详细的介绍。
论文[2]主要提出了CBOW和Skip-gram两种网络结构来训练词向量,并使用语义word relationship test和语法word relationship两种测试集来评估模型的有效性。
语义word relationship:$V(Athens)-V(Greece)+V(Norway)=V(Oslo)$
语法word relationship:$V(apparent)-V(apparently)+V(rapid)=V(rapidly)$
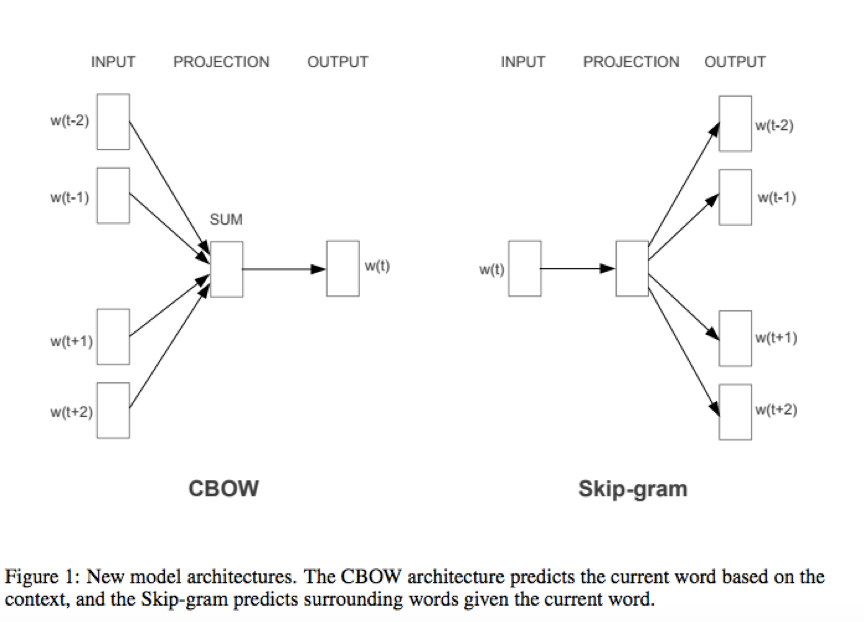
论文[3]提出了一些方法拓展CBOW和Skip-gram(为主)的词向量质量和训练速度,主要有:subsampling of frequent words;hierarchial softmax、negative sampling。Mikolov还指出Word2Vec的主要缺陷是无法感知语序和无法表达习惯用语(idiomatic phrases,即由若干个单词组成的约定俗成的短语,如 NewYork),对于idiomatic phrases,文中提出了一种简单的方法使得其词向量可训练(短语作为一个整体去训练)。
关于word2vec的数学原理请参考word2vec中的数学原理详解,讲得很详细也很透彻。
延续上文的思路,从目标函数和计算复杂度的角度看word2vec的发展。
CBOW的目标函数是:
\[\widehat{P}(w_{t}|w_{c})=\frac{e^{v_{w_{t}}^{T}v_{w_{c}}}}{\sum_{w=1}^{N}{v_{w}^{T}v_{w_{c}}}},\ where\ v_{w_{c}}=\sum_{i\in context(w_{t})}C(w_{i})\]损失函数是:
\[L(\theta)=-\frac{1}{T}\sum_{t}log\ \widehat P(w_{t}|w_{c})+R(\theta)\]计算复杂度是:
\[nm+mlog_{2}(N)=O(mlog_{2}(N))\]论文原文 $N\times D+D\times log_{2}(V)$
上式中N为语料中词的个数,N为语料中词的个数。
Skip-gram的目标函数是:
\[\prod_{-c\leq j\leq c, j\ne t}\widehat{P}(w_{j}|w_{t})=\frac{e^{v_{w_{j}}^{T}v_{w_{t}}}}{\sum_{w=1}^{N}{v_{w}^{T}v_{w_{t}}}}\]损失函数是:
\[L(\theta)=-\frac{1}{T}\sum_{t}\sum_{-c\leq j\leq c, j\ne t}log\ \widehat{P}(w_{j}|w_{t})+R(\theta)\]计算复杂度是:
\[n(m+nlog_{2}(N))=O(nmlog_{2}(N))\]论文原文 $C\times (D+D\times log_{2}(V))$
结论
NNLM到word2vec的发展使得计算复杂度由O(N)的线性级降低到对数级。
目前有很多开源工具提供词向量训练的功能:
- fasttext: facebookresearch/fastText, PS: fasttext是mikolov跳槽到facebook后开发的。
- gensim: gensim: topic modelling for humans
使用主流的深度学习框架训练词向量也并不困难:
- tensorflow的官方教程:Vector Representations of Words Tutorial
- Pytorch的官方教程:Word Embeddings: Encoding Lexical Semantics
未来
自从2013年Mikolov出词向量的概念后,NLP领域仿佛一下子进入了embedding的世界,Sentence2Vec、Doc2Vec、Everything2Vec。另一方面,研究人员也尝试使用其他的方法生成词向量,比如斯坦福NLP小组提出的Global Vectors for Word Representation 。
参考文献
[1] Bengio Y, Schwenk H, Senécal J S, et al. Neural Probabilistic Language Models[J]. Journal of Machine Learning Research, 2003, 3(6):1137-1155.
[2] Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013.
[3] Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]// International Conference on Neural Information Processing Systems. Curran Associates Inc. 2013:3111-3119.